L’analisi agli elementi finiti (FEM) è un metodo indispensabile per la previsione della tensione all’interno dei vari corpi. Oltre alle analisi classiche allo snervamento, è possibile anche effettuare analisi più complesse e dettagliate fino alla rottura, in modo da ottimizzare il materiale e i costi di produzione. Questo articolo esplora i principi fondamentali della rottura, le modalità principali (fragile, duttile e per fatica) e il ruolo della FEM nel modellare tali fenomeni. Vengono presentati i passaggi chiave della procedura FEM, dall’impostazione del modello geometrico all’interpretazione dei risultati.
di Carlo Augusto Pasquinucci
Introduzione
Nel campo dell’ingegneria strutturale, prevedere la tensione all’interno dei materiali e componenti è essenziale per garantire la sicurezza delle costruzioni. L’analisi agli elementi finiti (FEM) si è affermata come uno strumento indispensabile per modellare e analizzare strutture complesse, ma normalmente si utilizza ancora il limite allo snervamento per la maggior parte delle strutture. Questo comporta in molti casi a uno sovradimensionamento delle strutture. Da alcuni anni si sta sviluppando una nuova linea di pensiero che accetta che alcune parti possano snervarsi e addirittura rompersi, purché la struttura nel suo complesso rimanga funzionale o che almeno non crei danni ulteriori a persone o cose intorno in presenza di fenomeni violenti, ma molto rari, come per esempio terremoti o altre catastrofi naturali. Questo articolo esplora i principi fondamentali e le applicazioni pratiche dell’analisi FEM per la rottura, fornendo uno sguardo chiaro e accessibile per professionisti e appassionati di ingegneria.
I Principi della Rottura nei Materiali
La rottura avviene quando un materiale non è più in grado di sostenere le sollecitazioni applicate. Si distinguono tre principali modalità di rottura:
- Fragile: caratterizzata da una separazione rapida e senza significative deformazioni.
- Duttile: accompagnata da deformazioni plastiche prima della frattura.
- Per fatica: dovuta a carichi ciclici ripetuti.
Rispetto al semplice calcolo analitico, l’analisi FEM permette di simulare queste modalità utilizzando modelli teorici più complessi e avanzati. Tra i più comuni vi sono:
- Modelli di frattura elastici lineari (LEFM), usati per materiali fragili.
- Modelli elastoplastici non lineari, ideali per materiali duttili.
- Modelli di fatica, utili per studiare strutture sottoposte a sollecitazioni cicliche.
Procedura di Analisi FEM della Rottura
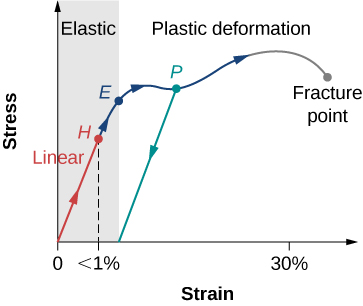
Per effettuare un’analisi FEM a rottura, bisogna ovviamente inserire oltre a tutti i dati per un’analisi FEM lineare (quindi con tensioni ammissibili fino allo snervamento), i dati della curva tensione-deformazione al di là dello snervamento e i criteri di rottura del materiale.
Innanzitutto, conviene comunque effettuare un’analisi preliminare a snervamento, per capire innanzitutto se le tensioni superano o no questo limite e soprattutto capire quali possano essere le zone più critiche, dove quindi bisogna effettuare una modellazione più accurata, con una griglia di calcolo più fitta e dettagliata.
L’analisi FEM, infatti, genera risultati che evidenziano:
- Zone critiche di stress: aree a rischio di rottura.
- Distribuzione delle tensioni: mappa di stress utile per identificare carenze progettuali.
- Previsione della propagazione delle crepe: fondamentale per la progettazione preventiva.
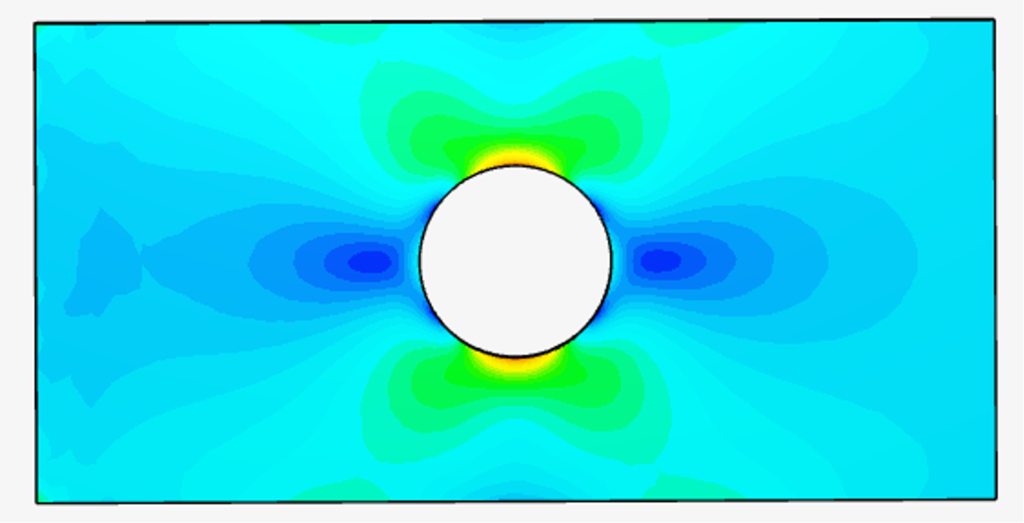
Un esempio pratico è l’analisi di una piastra metallica con foro centrale sottoposta a trazione. Il FEM mostra un’intensificazione delle tensioni intorno al foro, prevedendo la propagazione della frattura. Ovviamente, queste analisi preliminari ci danno informazioni su dove si potrà generare una rottura, ma per analisi più dettagliata è necessario modellare la rottura attraverso dei modelli matematici.
Criteri di rottura
I principali criteri di rottura che possono essere utilizzati in un’analisi FEM dipendono dal materiale e dalle condizioni operative. Tra i più comuni, si annoverano i criteri basati sulle tensioni che correlano il comportamento del materiale alle sollecitazioni indotte dai carichi applicati, i criteri basati sulle deformazioni, secondo i quali il materiale si rompe quando raggiunge una deformazione critica e quelli energetici, che si basano sull’energia necessaria a innescare o propagare una frattura. Ogni criterio è sviluppato per adattarsi a particolari materiali, modalità di cedimento o condizioni operative.
Criteri basati sulle tensioni
1. Criterio della Tensione Massima Principale
Secondo questo criterio, la rottura si verifica quando la massima tensione principale in un punto supera la resistenza del materiale a trazione o a compressione. Viene utilizzato principalmente per materiali fragili, come vetro, ceramiche e calcestruzzo, in cui la rottura è dominata dalla trazione. Ovviamente non considera gli effetti combinati delle tensioni principali, quindi può sottostimare lo stato tensionale del materiale in presenza di sollecitazioni da più direzioni.
2. Criterio di Tresca (Tensione di Taglio Massima)
Questo criterio prevede la rottura quando la massima tensione di taglio raggiunge il valore critico definito dal limite di snervamento del materiale. Viene utilizzato per materiali duttili, come acciai e leghe metalliche, che cedono per snervamento piuttosto che per rottura immediata. Non è adatto per materiali anisotropi o a quelli con comportamenti differenti in trazione e compressione.
3. Criterio di Von Mises (Energia Distorsionale)
Il criterio di Von Mises considera la rottura quando l’energia di deformazione distorsionale supera un valore critico. Questo criterio, più complesso, è perfetto per materiali isotropi e duttili, come acciai e alluminio. Inoltre, è molto accurato per analisi tridimensionali o per condizioni di carico complesse con diversi carichi in più direzioni. Purtroppo, non è molto adatto in caso di materiali fragili.
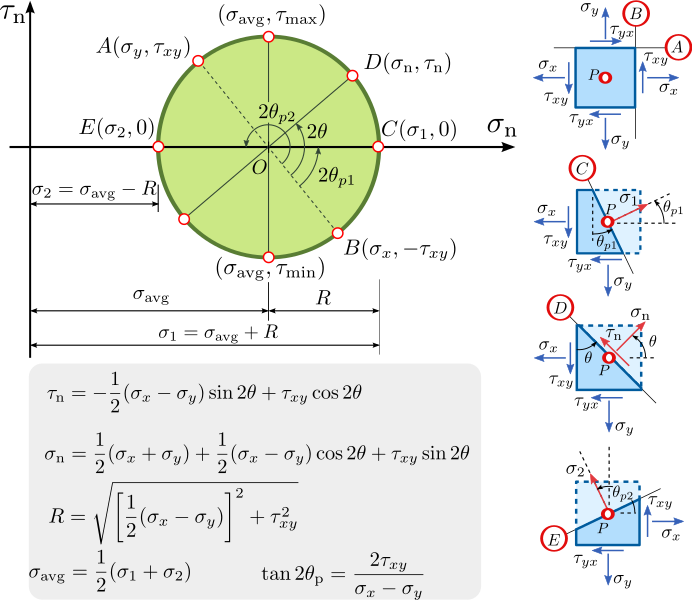
4. Criterio di Coulomb-Mohr
Il criterio di Coulomb-Mohr combina la resistenza a trazione e compressione del materiale per determinare la rottura, formulando un’equazione basata sulle tensioni principali. Per questo motivo, è perfetto per caratterizzare la rottura di materiali fragili con comportamenti asimmetrici in trazione e compressione.
Criteri basati sulle deformazioni
In alternativa, è possibile stabilire anche un criterio basato sulla deformazione massima ammissibile, al di là della quale si genera la rottura. Questi criteri sono rilevanti per materiali che tollerano elevate deformazioni plastiche, come elastomeri, polimeri e alcuni metalli duttili, per i quali, i criteri basati solo sulla tensione sarebbero poco precisi. Tra i principali si includono:
- Criterio della deformazione massima
La rottura si verifica quando la deformazione normale o tangenziale in un punto supera un valore critico definito dalle proprietà del materiale. È utilizzato principalmente per metalli duttili. - Criterio della deformazione specifica (o localizzata)
Considera la rottura come conseguenza di deformazioni eccessive concentrate in zone critiche, come punte di crepe o aree soggette a grandi gradienti di deformazione. Questo criterio è spesso adottato per simulare materiali con comportamento plastico marcato. - Criterio della deformazione principale
Si basa sulla valutazione delle deformazioni principali. La rottura avviene quando la massima deformazione principale (in trazione o compressione) raggiunge un valore limite. È utile per analizzare materiali anisotropi o fragili con comportamenti diversi sotto trazione e compressione. - Criterio di deformazione volumetrica
Analizza la deformazione volumetrica (cambiamenti di volume) per materiali che mostrano sensibilità al confinamento, come schiume o suoli. È usato nelle analisi di materiali granulari o strutture porose.
Criteri energetici
I criteri di rottura energetici rappresentano un approccio avanzato per la previsione del cedimento nei materiali, basandosi sull’energia necessaria a innescare o propagare una frattura. Questi metodi non si concentrano direttamente sulle tensioni o sulle deformazioni, ma analizzano la distribuzione e il bilancio dell’energia all’interno del materiale o della struttura. Sono particolarmente utili per studiare la propagazione delle crepe e il comportamento dei materiali sotto condizioni di carico estreme. I criteri energetici offrono un approccio potente e versatile per modellare il comportamento alla rottura, soprattutto in scenari complessi. La loro integrazione nei software FEM consente di analizzare dettagliatamente soprattutto i meccanismi di propagazione delle crepe, migliorando la progettazione strutturale e la sicurezza. Inoltre, è possibile predire in quanto tempo la cricca raggiungerà una dimensione tale da compromettere la sicurezza o la funzionalità del componente, aumentando quindi la vita utile e riducendo i costi di manutenzione. Tra i più diffusi, abbiamo:
1. Criterio della Energia di Frattura (LEFM)
Il criterio della frattura elastica lineare (Linear Elastic Fracture Mechanics, LEFM) si basa sul concetto di energia di frattura critica che rappresenta l’energia necessaria per far propagare una crepa per unità di superficie. È consigliato per materiali fragili come vetro, ceramiche e polimeri, dove il comportamento elastico domina fino alla rottura.
2. Criterio di Griffith
Formulato originariamente per materiali fragili, il criterio di Griffith postula che una crepa si propaghi quando l’energia rilasciata durante la sua crescita supera l’energia necessaria per creare nuove superfici.
Ovviamente questi criteri più complessi necessitano di più risorse computazionali e informazioni più accurate sui materiali, non sempre disponibili.
Rottura per fatica
La rottura per fatica è un fenomeno di cedimento progressivo che si verifica nei materiali sottoposti a carichi ciclici o ripetuti nel tempo, anche se le sollecitazioni applicate sono molto inferiori al limite elastico del materiale. È una delle principali cause di guasto in componenti strutturali, specialmente in settori come l’ingegneria civile, meccanica e aerospaziale. La fatica si sviluppa gradualmente, passando attraverso tre fasi distinte: innesco della cricca, propagazione della cricca, e rottura finale.
Meccanismo della Rottura per Fatica
- Innesco della cricca:
Questo stadio iniziale è causato da disomogeneità microscopiche nel materiale, come inclusioni, microfessure, o concentrazioni di tensione (ad esempio, spigoli vivi o fori). Le sollecitazioni cicliche creano deformazioni locali, favorendo la formazione di microcricche. - Propagazione della cricca:
Una volta che si è formata una cricca, essa si propaga lentamente ad ogni ciclo di carico. Durante questo processo, la cricca si allarga gradualmente, riducendo la sezione resistente del componente. La velocità di propagazione dipende dall’intensità del carico e dalle proprietà del materiale. - Rottura finale:
Quando la cricca raggiunge una dimensione critica, la sezione residua del materiale non è più in grado di sopportare il carico applicato. La rottura avviene improvvisamente, spesso in modo catastrofico, senza segnali evidenti.
Curva di Fatica: Il Diagramma S-N
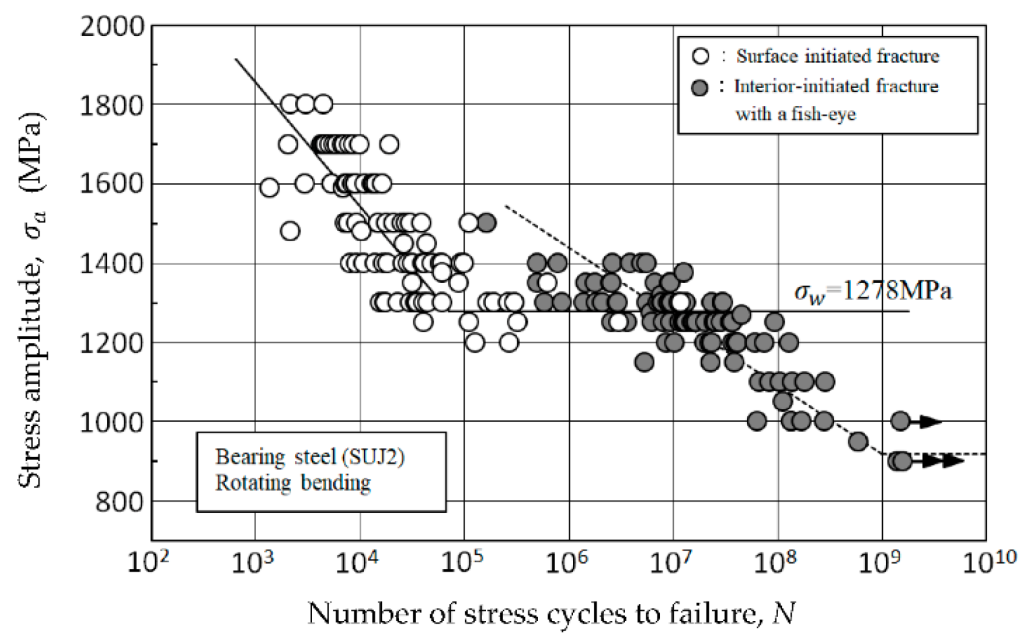
La resistenza alla fatica di un materiale viene comunemente rappresentata dal diagramma S-N, che mette in relazione l’ampiezza della tensione (SSS) con il numero di cicli (NNN) fino alla rottura.
- Regione a vita finita: Per carichi elevati, la rottura avviene dopo un numero relativamente basso di cicli.
- Regione a vita infinita: Al di sotto di un certo livello di tensione (detto limite di fatica), il materiale può teoricamente sopportare un numero infinito di cicli senza rompersi.
Normalmente, queste curve vengono effettuate per carichi alternati e con valore costante nel tempo, cosa che non sempre avviene nelle realtà. Ovviamente, con i programmi FEM, è possibile analizzare diverse fasi del ciclo di carico, in modo da calcolare la tensione massima e minima ma anche quelle nelle fasi intermedie. Non sempre questo è strettamente necessario e molto spesso conviene appunto effettuare il calcolo solo nelle condizioni più gravose. In questo modo, si considera un fattore aggiuntivo di sicurezza già nella modalità del calcolo.
È bene ricordare poi che la rottura a fatica si basa su teorie statistiche e quindi è buona norma considerare dei fattori di sicurezza maggiori rispetto al conto a snervamento.
Per tenere conto di cicli di carico differenti, i software di analisi FEM rendono poi possibile anche utilizzare modelli matematici più complessi, come il modello basato sull’energia della frattura (Fracture Mechanics Model) che concentra sull’analisi della propagazione delle cricche all’interno di un materiale. In particolare, esplora come le microfessure si evolvono sotto carico, portando alla rottura del materiale nel tempo. Questo permette anche di prevedere la vita residua di un componente soggetto a carichi ciclici, consentendo di valutare quando una cricca potrebbe raggiungere una dimensione critica, portando alla frattura catastrofica del materiale.
Ovviamente, analisi più complesse richiedono potenza e tempi di calcolo maggiori, ma soprattutto uno maggior numero di dati e una maggiore precisione degli stessi.
Conclusioni
In questo articolo abbiamo brevemente esplorato la rottura dei materiali. Ovviamente, la maggior parte delle analisi strutturali utilizza come criterio di accettazione l’assenza di snervamento, ma per avere un’ottimizzazione del materiale e quindi una riduzione dei costi, sempre più aziende richiedono analisi a rottura. Per calcoli sempre più complessi sono necessari software FEM avanzati, che permettano di utilizzare criteri di rotture basati su formule matematiche complesse. Grazie ai continui progressi nei modelli matematici e nei software, le applicazioni di questa tecnica continueranno ad espandersi, rivoluzionando il modo in cui progettiamo e valutiamo le strutture.





